Basic Consumer Theory

#economics #micro

Oh, Hyunzi. (email: wisdom302@naver.com)
Korea University, Graduate School of Economics.
2024 Spring, instructed by prof. Koh, Youngwoo.

Consumption Set

  • : number of goods
  • : consumption bundle, commodity vector
  • : consumption set, the set of all conceivable consumption bundles.
  • : Budget constraint, set of all affordable consumption bundles for given price and income .
Proposition (convexity of the budget set).

is convex set.

Proof. Let . WTS we show (i) such , and (ii) .

  • (i) since , and , we also have as .
  • (ii) since , by the def of the budget constraint, we have therefore, we have thus .
    therefore, is convex. □

Preferences and Utility

  • : preference relations. a binary relation on to order the bundles .
    • : is at least as good as , weak preference.
    • : is strictly preferred to , strict preference.
    • : is indifferent to , indifference.
  • Subsets of
    • : Upper contour set
    • : Lower contour set
    • : Indifference set(curve)
    • : Strictly upper contour set
    • : Strictly lower contour set
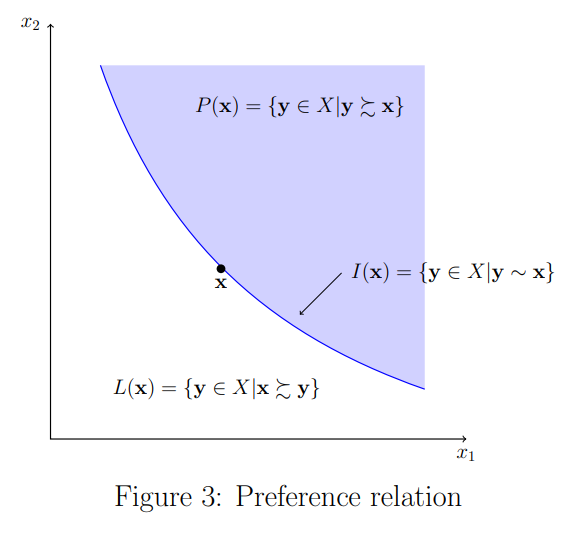
    • Pasted image 20240308173905.png
Definition (rationality).

A preference relation on is rational if

  • complete: for every bundle, the order is defined.
  • transitive: from the consecutive two relations, we can derive a new relation.
rational preference?
  • complete: 모든 소비 조합에 대해 선호 체계 정의되어 있음.
  • transitive: 정의된 선호 체계가 전체적으로 모순되지 않음.

Other properties of :

  • monotone: a larger amount of commodities are more preferred.
  • strict monotone:
  • continuous: there is no sudden jump on preference.
    • equivalently, for any ,
  • Lexicographic preference violates continuity:
    • for the sequence of bundles and . while we have , we have , a contradiction.
    • Pasted image 20240308183953.png
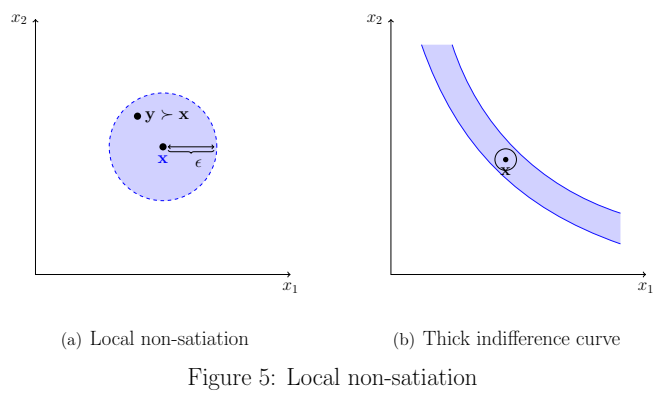
  • nonsatiated: for any given bundle, there always exists another bundle that is more preferred.
    • if the budget is infinite, then the consumer is never be 'satisfied', i.e. maximized.
  • local nonsatiated: for any small distance, there always exists another bundle that is more preferred.
    • by the local non-satiation, any 'thick' indifference curve cannot happen.
    • Pasted image 20240308183556.png
  • convex: for any two bundles, the convex combination bundle of two is at least as good as one of them.
    • convexity implies the diminishing marginal rates of substitution.
    • when decreasing goods by 1 unit, to maintain the same amount of utility, goods must be increased by 1 unit or more.
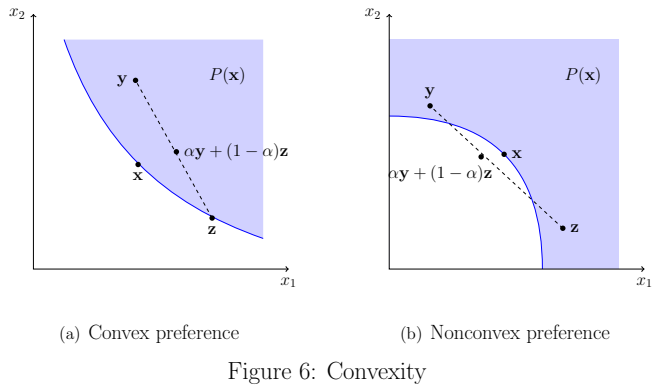
    • Pasted image 20240308230315.png
  • strict convex:

Utility Function

Definition (utility function).

A utility function represents the preference relation if and only if .

Example (examples of utility function).
  • Cobb-Douglas: where . then is continuous & strict monotone, & strict convex.
  • Linear: . then is continuous & strict monotone, & convex.
  • Leontief: . then is continuous, & (weak) monotone, & convex.
Proposition (utility function preference relation).

if a preference relation can be represented as a utility function , then it is rational.

Proof. ASM be the utility function representing . i.e. WTS is (i)complete, and (ii)transitive.

  • (i) note that , and is a complete metric space. and let . then we have
  • (ii) let and & by (i). WTS must hold. we have thus the preference relation is rational. □

Existence of utility function

Theorem (preference relation utility function).

if a preference relation is complete, reflexive, transitive, continuous, and strictly monotonic, then there exists a continuous utility function that represents .

Proof. Let , and . now let s.t. WTS: that there exists such continuously.

Let and .
we show that s.t. , i.e. , equivalent to .

  1. Existence of :
    • trivially, and by the strict monotone, as , and similarly for the other case.
    • by the completeness of , since the preference is defined in all .
    • now we show that are both closed, while . which follows to that .
    • first we show that is closed. i.e., every sequence converges to some .
      • ASM some sequence , where .
      • since , we have .
      • by the def of , we have .
      • as is continuous, is closed. thus .
      • therefore , establishing is closed.
    • similarly, we show that is closed.
      • ASM some sequence , where .
      • since , we have .
      • by the def of , we have .
      • as is continuous, is closed. thus .
      • therefore , establishing is closed.
    • thus and cannot be disjoint, which means there exists s.t. , i.e. .
  2. Uniqueness of :
    • ASM and . then by transitivity of , we have . i.e., both and .
    • recall Def of strict monotone:
    • then by the strict monotonicity, we have , which means , meaning that is unique.

since there exists a unique to every , we can map a function from to , i.e. a utility function that represents .
furthermore, by letting: , by the Definition 3 (utility function).
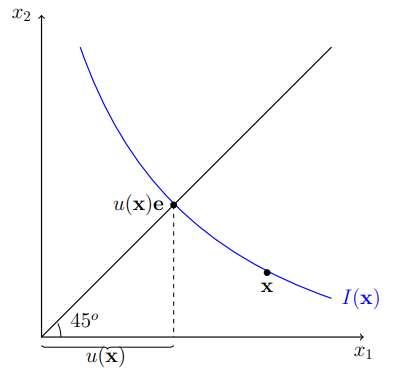
Pasted image 20240309214027.png

  1. Continuity of :
    • by check for continuous 2, a utility function is continuous if is open for all .
    • note that
    • thus ISTS that both and are open, as the intersection of two open set is open.
    • firstly, we show is open:
      • from the def of , we have .
      • thus we have
      • since is continuous, is open.
    • secondly, we show is open.
      • similarly, we have
      • since is continuous, is open.

by combining the two, is open, thus leads to that is continuous. □

Example (non-representation of Lexicographic Preference).

Note that the Lexicographic Preference defined as: cannot be representative by any function whether continuous or not.

Proof.

  • RTA that represents Lexicographic.
  • for any real number , there exists a rational number s.t. , where .
  • if , then we have some s.t. . thus the mapping from to is one-to-one
  • however, it is a contradiction since there is no one-to-one mapping between real numbers and rational numbers.
    thus the Lexicographic preference is non-representatable. □

Monotone Transform

by using the monotonic function, we can transform the utility function into the other form of utility function representing the same preference.

Theorem (utility function and monotonic transforms).

If represents some preference and is strictly increasing, then represents the same preference.

Proof. ASM that there exists some representing . then by Definition 3 (utility function), we have since is strictly increasing, we have which completes the proof. □

Example (monotone transform of Cobb-Douglas Utility).

from Cobb-Douglas Utility function,

  1. for , we have
  2. for , we have

Properties of Utility Function

The Utility function inherits the properties of the preference relation.

Theorem (properties of utility function).

Let . then we have the following properties.

  • is strictly increasing iff is strictly monotonic.
  • is quasi-concave iff is convex.
  • is strictly quasi-concave iff is strictly convex.
Definition (marginal utility and marginal rate of substitution).

Let be a given bundle.

  • Marginal Utility(MU) of : the rate of change in utility due to a marginal increase in one good only.
  • Marginal Rate of Substitution(MRS) of for : the amount of that is required to give up for to maintain the same utility level.
    • the absolute value of slope of indifference curve at .
    • MRS is preserved to monotone transforms: for ,
Remark (Implicit Function Theorem and MRS).

Let . and be the utility level s.t. then by the Implicit Function Theorem, thus

Utility Maximization and Optimal Choice

A rational consumer will choose a most preferred bundle from the set of affordable alternatives(budget constraint).

Utility Maximization Problem (UMP)

Proposition (UMP).

for and , Utility Maximization Problem(UMP) is defined as and if is continuous, then since is compact, by the Weierstrass thm, at least one solution exists.

Marshallian Demand Correspondence

Definition (Marshallian demand correspondence).

Proposition (properties of Marshallian demand).

If is continuous and corresponding is locally non-satiated on . then the Marshallian demand correspondence satisfies the following properties:

  1. Homogeneity of degree zero (HOD0):
  2. Walras' law:
  3. Convexity and Uniqueness: if is quasi-concave, then is convex. Moreover, if is strictly quasi-concave, then is has a unique value.
  4. Hemicontinuity and Continuity: If is quasi-concave, then is upper-hemicontinuous at . Moreover, if is strictly quasi-concave, then is continuous at .

Proof.

  1. ISTS that is HOD0, i.e. .
    • let is given arbitrage.
    • then , and .
    • by def, we have
    • since , we have .
    • thus we have .
  2. WTS .
  3. Let
    1. WTS#1 if is quasi-concave, then is convex
      • ASM is quasi-concave, i.e. where .
      • since , we have
      • therefore is convex.
    2. WTS#2 if is strictly quasi-concave, then is singleton set.
      • RTA: let .
      • since is strictly quasi-concave, we have
      • thus this contradicts with the def of , where gives the optimal utility.
      • therefore must be a singleton set.
  4. Follows directly from the Berges' Maximum Theorem.

this completes the proof □

  • if preference if not strictly convex, then demand is an upper-hemicontinuous correspondence.
    Pasted image 20240316222059.png
  • if preference is strictly convex, then demand is a continuous function.
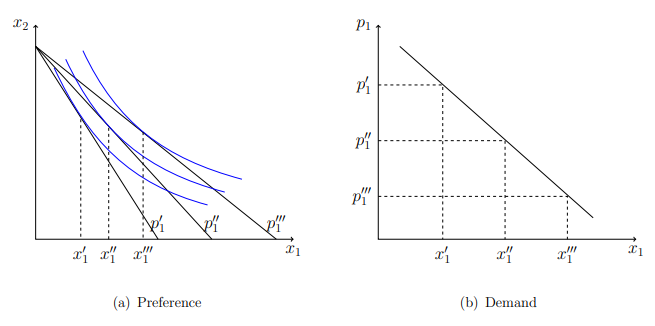
    Pasted image 20240316222210.png

Indirect Utility Function

Definition (Indirect Utility Function).

for the given Marshallian demand correspondence , the indirect utility function is defined as

Tip

indirect utility function returns the possibly achievable optimal utility under given price and budget set, which equals to the utility of choosing demand() s.t. solution of UMP.

Proposition (Properties of the Indirect Utility Function).

If is continuous and its corresponding is locally nonsatiated, then the indirect utility function is

  1. Homogeneous of degree zero (HOD0).
  2. Nonincreasing in , and strictly increasing in .
  3. Quasiconvex in and .
  4. Continuous in and .

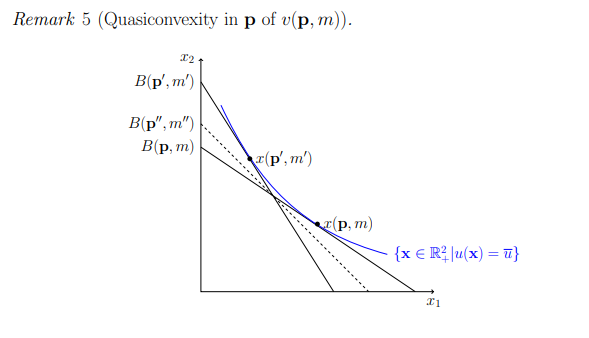
Pasted image 20240320172221.png

Proof.

  1. WTS , .
  2. WTS , , and , .
    • note that .
    • first we show the nonincreasing in .
      • thus for , we have .
      • then, we have
    • next we show the strictly increasing in .
      • thus for , we have .
      • since the corresponding is locally nonsatiated, we have s.t for all .
      • thus we have
  3. let , WTS
    • first we show .
      • RTA: ASM s.t. .
      • thus such satisfies that while and .
      • thus which leads to a contradiction.
    • next, we have
  4. Follows directly from the Berges' Maximum Theorem.

this completes the proof. □

Lagrangian Method

Proposition (Lagrangian Method).

let the maximization problem the corresponding Lagrangian function is where is Lagrange multiplier (non-negative).
if , then the Complementary-Slackness conditions(CS) is where .
if , then UMP has interior solution: if the solution is boundary(not interior):

Example (Demand Function for Cobb-Douglas Utility).

given the utility function , UMP is

Proof.
Lagrangian function: CS conditions: Check for the boundary solutions: thus if , then . thus must hold.
similarly, thus if , then . thus must hold.
therefore, from the CS conditions, we have Solution of UMP:
since , we have combining the two, since , the demand function for each is Therefore, the indirect utility function is □

Example (Demand Function for Quasi-linear Utility).

given the utility function the UMP is

Proof.
Lagrangian function: CS conditions: Check for the boundary solutions: thus is not rejected, meaning that .
similarly, thus if , then , which means , i.e. by CS condition.

Solution of UMP:
since , we have thus therefore, by CS , must hold. thus from CS, we have now we consider the case whether or .

  • Case#1 : then by CS, must hold. therefore we have furthermore, we have then only if .

  • Case#2 : then we have therefore we have then only if .

In sum, the optimal solution is given by which is the demand function for the given utility function. □

Pasted image 20240318162834.png

Example (Demand Function for non-linear Utility).

given the utility function the UMP is

Proof.
Lagrangian function: CS conditions: Check for the boundary solutions: thus if , then , which means , i.e. .
similarly, thus if , then , which means , i.e. by CS condition.

Solution of UMP:
since , we have thus therefore, by CS, . then the demand function is furthermore, the indirect utility function is which completes the proof. □

Comparative Statistics of Demand Functions

Assume that is single valued, i.e., a demand function.

Wealth Effect

  • wealth effect for -th good:

    • 자산의 한 단위 변화가 소비에 미치는 영향

  • wealth effect for :

  • elasticity of demand with respect to wealth:

  • commodity is normal at if

    • non-increasing in .

  • commodity is inferior at if

  • normal demand: every commodity is normal

Price Effect

  • price effect of on the demand for good :

  • price effect of on :

  • elasticity of demand with respect to -th price:

  • commodity is giffen good at if

Aggregated Effects

Proposition (cancellation of wealth and price effects).

if the demand function is HOD0, then for all , we have or i.e.,

the proposition directly follows from the def of HOD0. this implies that, when we increase all prices and wealth proportionately, then the price and wealth effects are cancelled out, thus the demand will be preserved at the initial level.

HOD0?

만약 이 동일 상수배로 변화할 경우 전체 수요량은 변하지 않는다 (HOD0의 의미). 이는 곧 가격 상승(하락)에 따른 영향이 실질임금 하락(증가)에 대한 영향으로 상쇄되기 때문이다.

Remark (@Proposition 22 (cancellation of wealth and price effects)).

from LHS, since for all , is assumed, implies that i.e. equal percentage change in all prices and wealth does not effect in demand.

Proposition (Cournot aggregation).

if satisfies Walras' law, then for all , we have or i.e., this implies that where .

interpretation

i.e.

Proof. WTS .
by the Walras' law, we have i.e. taking on both sides, we have where the last equation holds from the definition this completes the proof. □

Proposition (Engel aggregation).

if satisfies Walras' law, then for all , we have or i.e., this implies that where .

interpretation

자산 변화에 따른 총소비 변화량의 합은 자산 변화 단위와 같다.

Proof. WTS: .
by the Walras' law, we have i.e. taking on the both sides, we have where the last equation holds from the definition of this completes the proof. □

Walras law?

Walras' law에 따라 전체 L개 재화가 있을 경우, L-1개 재화 시장이 청산(clear)될 경우 나머지 하나의 시장은 자동으로 청산된다.
Cournot & Engel: 총소비는 가격 변화에 의해 영향 받지 않으며, 오로지 자산의 변화에 의해서만 변화한다.

Expenditure and Hicksian Demand Functions

Expenditure Minimization Problem (EMP)

Proposition (EMP).

for and , Expenditure Minimization Problem(EMP) is defined as and if is differentiable, the optimal consumption bundle can be characterized using first-order conditions, where is a Lagrangian multiplier.

the proof is similar to Lagrangian Method.

Proof.From the EMP, we have Then the Lagrangian is Then by the Kuhn-Tucker condition, the first-order conditions are that there exists and such that that is, for some , we have which completes the proof. □

Example (EMP for Cobb-Douglas utility function).

as given in Example 19 (Demand Function for Cobb-Douglas Utility), solve EMP s.t.

Proof.
Lagrangian: since and are not binding (see Example 19 (Demand Function for Cobb-Douglas Utility) for excluding the corner solution).

Assuming an interior solution:

thus therefore, from we can derive the hicksian demand function: and the expenditure function is, this completes the proof. □

Expenditure Function

Definition (Expenditure Function).

for the given Hicksian demand function , the expenditure function is defined as

Tip

expenditure function returns the possibly achievable optimal utility under given price and budget set, which equals to the utility of choosing demand() s.t. solution of UMP.

Proposition (Properties of the Expenditure Function).

If is continuous and locally non-satiated on , then is

  1. Homogeneous of degree 1 in .
  2. Strictly increasing in and nondecreasing in .
  3. concave in .
  4. continuous in and .

Proof.

  1. WTS for all scalar , .
  2. WTS , and , .
    1. first we show the strictly increasing in .
      • RTA: ASM is not strictly increasing in .
      • ASM: for , let for some .
      • let , for .
      • since is continuous,
      • this contradicts to the assumption that , since it is not sol of EMP.
    2. next we show the nondecreasing in .
      • ASM: let .
      • then we have
  3. for a fixed , and let and . WTS
    • as is the minimum expenditure for any , we have
    • therefore, we have
    • thus is concave in .
  4. This directly follows from Berges' Maximum Theorem.

this completes the proof. □

Hicksian Demand Function

Definition (Hicksian demand function).

Proposition (Properties of Hicksian demand I).

If is continuous and locally nonsatiated, then for , hicksian demand function is

  1. Homogeneous of degree 0 in .
  2. no excess utility.
  3. if is quasi-concave, then is convex. Moreover, if is strictly quasi-concave, then is has a unique value.

Proof.

  1. WTS: for any scalar , .
  2. WTS: , .
    • RTA: ASM , for some .
    • let , for all .
    • since is continuous,
    • thus we have which is a contradiction to ASM that .
    • therefore must hold for every .
  3. Let
    1. WTS#1 if is quasi-concave, then is convex
      • ASM is quasi-concave, i.e. where , for all .
      • since , we have where , .
      • then we have
      • also, as is quasi-concave, therefore we have , i.e. is convex.
    2. WTS#2 if is strictly quasi-concave, then is singleton set.
      • RTA: let .
      • ASM: is strictly quasi-concave, we have where , for all .
      • note that where since , we have
      • thus this leads to a contradict, therefore must be a singleton set.

this completes the proof. □

Relationships

Dual Problems

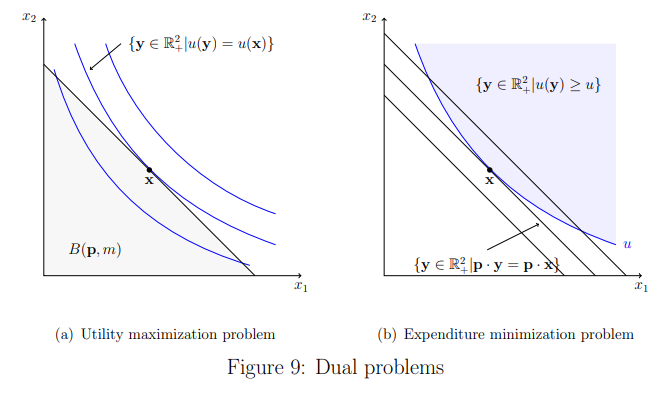
Pasted image 20240322222151.png

UMP and EMP yields to the same solution.

  1. optimal UMP is optimal EMP
    • first, maximize utility under the given budget restraint.
    • next, using the maximized utility as a lower bound, minimize the expenditure.
    • then the optimal demand for EMP is exactly the solution for UMP.
  2. optimal EMP is optimal UMP
    - first, minimize expenditure under the given utility level.
    - next, given the minimized budget restraint, maximize the utility.
    - then the optimal demand for UMP is exactly the solution for EMP.
    the formal proposition is stated as follows.
Proposition (duality).

Let is continuous and locally nonsatiated. and let the price vector . then the duality of UMP and EMP holds.

  1. If is optimal UMP when . then is optimal in EMP when utility level is . Moreover, the minimized expenditure level in EMP is exactly .
  2. If is optimal EMP when required utility is . then is optimal UMP when wealth is . Moreover, the maximized utility in UMP is exactly .

Proof.ASM is continuous and locally nonsatiated.
WTS#1: UMP implies EMP

  • ASM is solution for UMP, when and .
  • RTA suppose is not EMP, i.e.
  • since is locally nonsatiated, where .
  • for such , we have therefore we have which is a contradiction to ASM that is optimal UMP.
  • therefore is sol for EMP.
  • furthermore, by the Walras' law, we have .

WTS#2: EMP implies UMP

  • ASM is sol for EMP for given .
  • RTA suppose is not UMP, where . i.e.
  • now let , where .
  • since is continuous, for , we have thus is not sol for EMP, which is a contradiction.
  • therefore must be optimal UMP when wealth is .
  • furthermore, the maximized utility in UMP is .

this completes proof. □

Relationships

Theorem (Demand, Indirect utility, and Expenditure).

Let is continuous and strictly increasing. then for all , and we have the following relations:

  1. .
  2. .
  3. .
  4. .

Proof. Let is continuous and strictly increasing.
WTS#1 .

WTS#2 .

  • first .
  • next, .
    • RTA suppose .
    • since is continuous, then is also continuous.
    • then there exists some small , that satisfies which is a contradiction to that since .
    • thus we have .

WTS#3 .

WTS#4

this completes the proof. □

Example (relationships under Cobb-Douglas utility).

Proof.Consider the previous examples:
from Example 19 (Demand Function for Cobb-Douglas Utility), we have and also, from Example 27 (EMP for Cobb-Douglas utility function), we have and

WTS#1 .
WTS#2 .
WTS#3 .
WTS#4
this completes the proof. □

Hicksian and Expenditure

Proposition (Shephard's lemma).

If is continuous, locally nonsatiated on , and strictly quasiconcave, then we have i.e.

Proof. note that , by the definition.
FOC approach:
for any , let s.t. and , . and note that then we have similarly, we have combining the two inequalities, we have since is continuous in , (see Proposition 29 (Properties of the Expenditure Function)), we have thus we have .

Envelope Theorem approach:
note that
Theorem 30 (Envelope Theorem).

Let a function of . for the maximization problem let be a solution problem. and let . now suppose . then we have Pasted image 20240317202812.png


let be the solution for the EMP. and let the Lagrangian function as and let for a saddle point , where . since are both continuous, by the envelope theorem, we have this completes the proof. □

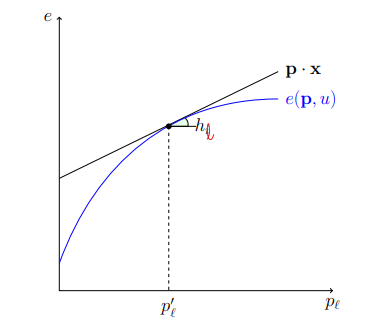
Pasted image 20240322171735.png

  • let is the optimal consumption for EMP given and .
  • then at , the change of the expenditure with respect to equals to the partial derivatives of the objective function, which is denoted as Hicksian demand function.
Proposition (Properties of Hicksian demand II).

The substitution matrix defined as satisfies

  1. i.e., .
  2. , or is negative semidefinite.
  3. , or is symmetric.
  4. . i.e., .
  1. from , we have
    • in matrix form, from , we have
  2. note that is concave in and (Proposition 29 (Properties of the Expenditure Function))
  3. by the definition of Hessian matrix, is symmetric.
  4. note that is HOD0 (Proposition 31 (Properties of Hicksian demand I))
    • as is HOD0, we have
    • by differentiating the both sides with , we have

this completes the proof. □

Corollary (Properties of Hicksian demand III).

For each good , it holds that

  1. : (compensated) own price effect is nonpositive.
  2. for all : cross price effects are symmetric.
  3. for some : each good has at least one substitute.

this properties directly follows from the fact that Hessian matrix is negative semidefinite, symmetric, and .

Hicksian and Marshallian Demand

Theorem (Slutsky Equation).

Let is continuous, locally nonsatiated, and strictly quasi-concave. then for all , we have i.e.

Proof.Let , and .
by Theorem 33 (Demand, Indirect utility, and Expenditure), we have the relation of by differentiating the both side with , we have where the third equality holds by Proposition 35 (Shephard's lemma), and the fourth equality holds by Theorem 33 (Demand, Indirect utility, and Expenditure). □

Slutsky equation

Slutsky equation implies that the total change in demand can be decomposed as substitution effect and the income effect.

  • : substitution effect, measures the change in demand due to the change in its relative price.
  • : income effect, measures the change in demand due to the change in the 'purchasing' power.
  • : price effect, change in demand due to the change in its price. combined result of substitution and income effect.

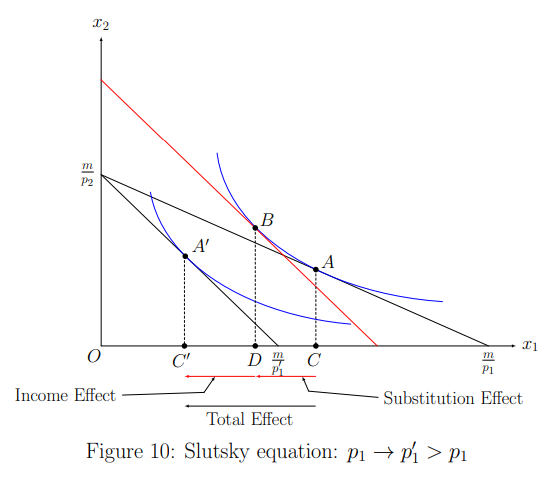
Pasted image 20240323131439.png

Remark (Slutsky substitution matrix).

from Theorem 38 (Slutsky Equation), we have where note that as stated in Corollary 37 (Properties of Hicksian demand III), is symmetric and negative definite, while .

  • if price changes, goods' Hicksian (compensated) demand changes by the sum of
    1. price effect of
    2. income effect (by the change in wealth to maintain the prior consumption).
  • since is negative definite, we have for all .
    • the substitution effect by the change of the price itself, i.e., the partial derivatives of Hicksian demand function with respect to its price is always negative.
    • simple reason is that indifference curves are always downward sloping.
    • note that Hicksian demand function measures the optimal consumption under given , allowing the changes in . thus without losing purchasing power, the increase in its own price will always decrease demand on itself.
  • equivalently, in terms of elasticity, where denotes the budget share.

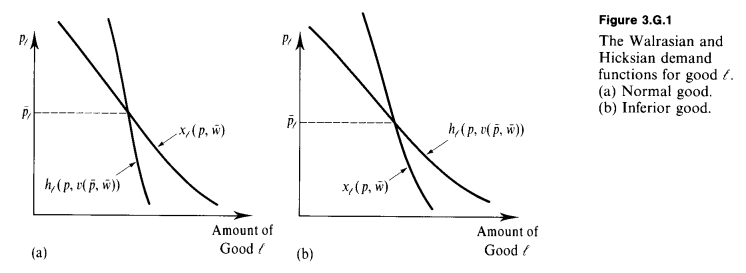
Pasted image 20240323140833.png
let be fixed except .

Total Effect
:		 Substitution Effect
:		 Income Effect
:
(+) substitute(+) normal(+)
(-) complementary(-) inferior(-)

Compensated law of Demand

Definition (WARP).

let be a single valued function, HOD0, and satisfies Walras' law. satisfies the Weak Axiom (WA) if for any , we have

WA implies that if the consumer choose even if is also consumable, then can be chosen only if is not available.

Proposition (compensated law of demand).

let is single valued function, HOD0, and satisfies Walras' law. then it satisfies Weak Axiom if and only if for every price change to s.t. the following inequality holds and the strict inequality holds if .
equivalently, in matrix form,

Proof.We only look for the matrix version.
suppose . then from , we have thus where the last inequality holds since , Slutsky substitution matrix is negative semidefinite by Remark 39 (Slutsky substitution matrix). □

the proposition means that for any compensated price changes, the law of demand (price changes and demand changes have different signs) hold, i.e. compensated law of demand.

Tip

note that the price change can be decomposed into two parts:

  • relative price effect = substitution effect
  • real wealth effect = income effect

and by adjusting wealth by , we can make (real wealth effect is) compensated price changes, which holds the law of demand.

Marshallian and Indirect Utility

Theorem (Roy's Identity).

Let is continuous, locally nonsatiated, and strictly quasi-concave. and let the indirect utility function is differentiable where . then we have i.e.

Proof.From the prior identity, let . by differentiating with respect to , we have where the second equality holds by Shephard's lemma and the last equality holds by identity theorem.
therefore we have this completes the proof. □

note that by meaning of Lagrangian constant, we have thus the Roy's identity is equal to i.e. meaning that the first derivative of the indirect utility function equals to the demand function multiplied by 'marginal utility of wealth at optimum'.

Relationships between EMP and UMP

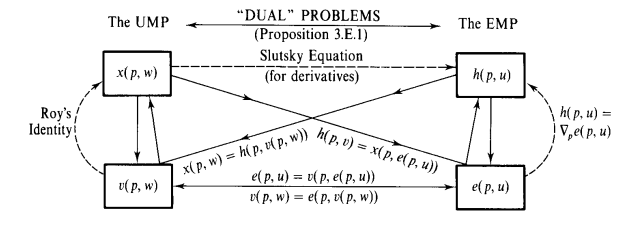
Pasted image 20240322222631.png

The above figure summarizes the connection between the demand and value functions driven from Dual problems.

Interactive Graph
Table Of Contents
Basic Consumer Theory
Consumption Set
Preferences and Utility
Utility Function
Existence of utility function
Monotone Transform
Properties of Utility Function
Utility Maximization and Optimal Choice
Utility Maximization Problem (UMP)
Marshallian Demand Correspondence
Indirect Utility Function
Lagrangian Method
Comparative Statistics of Demand Functions
Wealth Effect
Price Effect
Aggregated Effects
Expenditure and Hicksian Demand Functions
Expenditure Minimization Problem (EMP)
Expenditure Function
Hicksian Demand Function
Relationships
Dual Problems
Relationships
Hicksian and Expenditure
Hicksian and Marshallian Demand
Compensated law of Demand
Marshallian and Indirect Utility
Relationships between EMP and UMP